Éléments mathématiques ….
Il s’agit de résoudre une série d’équations appelées différentielles, une pour chaque membre de la filiation. Pour un membre donné, l’équation est obtenue en écrivant que la variation du nombre d’atomes est égale à la différence des noyaux qui sont formés à partir de la désintégration du père et ceux qui disparaissent en se transformant en noyau fils. Pour un radioélément donné, le nombre de noyaux qui disparaissent par seconde est égal à l’activité a = λ N, où N représente le nombre de noyaux présents de l’espèce radioactive (NB : la probabilité de désintégration λ est déduite simplement de la période radioactive T : λ = 0,693/T).

Entrée des données
Les données à entrer sont indiquées en jaune sur la page des calculs EXCEL comme indiqué sur l’exemple. Pour chaque membre de la filiation (jusqu’à 4) on introduira, le numéro atomique A, la charge du noyau Z, la période en années, et la masse en kilogramme. Pour les diagrammes, on choisira l’unité pour les activités, les maxima des temps envisagés pour les échelles de temps linéaires et logarithmiques.
©IN2P3
En absence de régénération du noyau, on observe une décroissance simple en fonction du temps selon une loi en exp(-λt) appelée exponentielle. Dans le cas plus général d’une filiation naturelle, la solution de l’équation différentielle est une combinaison des exp(-λt) propres à chacun de ces ancêtres. La combinaison est déterminée à partir des données connues au départ. Dans le cas des réacteurs en fonctionnement, les noyaux radioactifs sont également produits à partir de captures de neutrons. Il faut modifier le terme source.
Par exemple, si l’on s’intéresse à la filiation d’un échantillon initialement pur d’uranium-238, toutes les activités des descendants sont nulles au départ. L’activité du “patriarche”, l’uranium-238, est calculée à partir de sa masse dans l’échantillon.
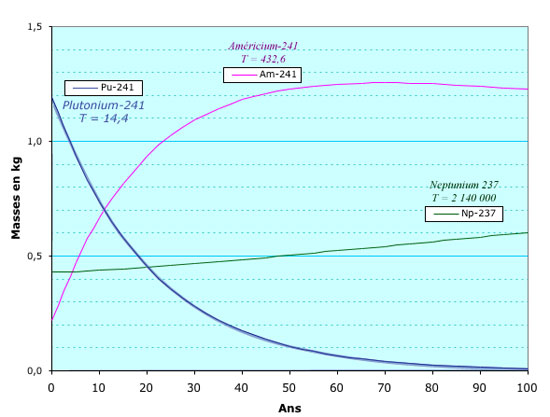
Exemple 1 : évolution des masses
Le plutonium-241, l’américium-241 et le neptunium-237 étant présents au départ en quantité notable, on a représenté ici l’évolution de leur masse. L’échelle de temps a été choisie de 0 à 100 ans. Pour représenter cette évolution à une autre échelle, il faut changer le temps maximum dans la feuille de calcul EXCEL.
© IN2P3
Exemple 1 : Filiation dans un combustible usé
L’exemple montre l’évolution d’un mélange de plutonium 241, d’américium-241 et de Neptunium-237, trois actinides de la famille (4n+1) présents dans le combustible usé des réacteurs. Les quantités initiales sont tirées de la composition détaillée d’une tonne de combustible. Les trois radioéléments sont présents au départ. A l’échelle de 100 ans, le noyau père (plutonium-241) a le temps de disparaître à peu près complétement ; l’américium commence à croître (alimenté par les désintégrations du plutonium) avant de décroître. Quant au Neptunium, alimenté par la désintégration de l’américium, il faudrait attendre des millénaires pour commencer à voir sa décroissance.
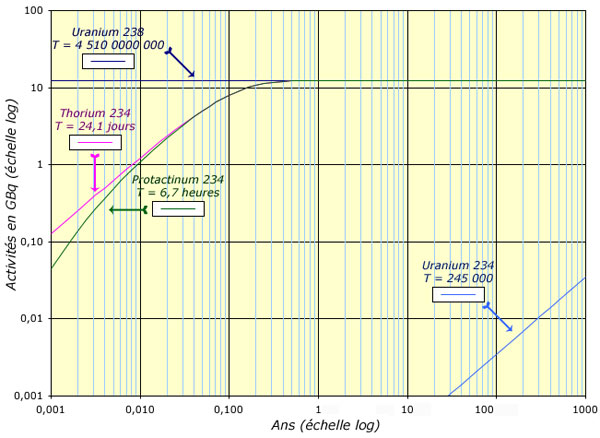
Début de la filiation de l’uranium 238
Représentation à 1000 ans de l’activité des premiers descendants de l’uranium. Du fait de la période très longue de l’uranium-238 (4,5 milliards d’années) et celles très courtes du thorium-234 et du protactinium-234 (24 jours et 7 heures) il faut employer des échelles logarithmiques pour voir ces deux descendants atteindre en une fraction d’année l’équilibre radioactif. Au bout de 1000 ans le troisième descendant, l’uranium 234 (période 245 000 ans) est encore très loin de l’équilibre.
© IN2P3
Exemple 2 : Début de la filiation de U-238
L’exemple montre que les premiers descendants à courte période de l’uranium (44 jours et 6,7 heures) atteignent très vite l’équilibre radioactif et que au bout de quelques mois leur activité est devenue égale à celle de l’uranium. Pour observer l’évolution sur des temps allant de quelques heures à des milliards d’années il faut employer des échelles logarithmiques.

Suite de la filiation de l’uranium 238
A l’échelle choisie du million d’années, on observe l’arrivée à l’équilibre des trois descendants de longue vie, l’uranium-234, le thorium-230 et le radium. Sur le graphique, la courbe du radium dont la période n’est que de 1500 ans ne peut être distinguée de celle de son père le thorium 230 (T=75000 ans). Il en va de même pour tous les descendants du radium qui sont à vie courte.
© IN2P3
Exemple 3 : Suite de la filiation de U-238
Les activités des descendants de courte durée s’identifient rapidement à celle de leur premier ancêtre à vie longue. L’exemple montre la lente arrivée à l’équilibre à l’échelle du million d’années des deux descendants à vie longue de l’uranium 238 : l’uranium 234 (T=245 000 ans) et le thorium 230 (T= 75 000 ans).
Voir aussi :
Mathématiques des filiations radioactives (pdf)
Exemple 1 : Filiation Pu-241 (xlsx)
Exemple 2 : Début de la filiation U-238 (xlsx)
Exemple 3 : Suite de la filiation U-238 (xlsx)
Les autres articles sur le sujet « Périodes et activités »
Période radioactive
La mesure de la rapidité de la décroissance La loi de décroissance radioactive a été formulée dès[...]
Activité radioactive
Taux de désintégrations et de rayonnements émis L’activité d’un échantillon de matière radi[...]
Filiations radioactives
Radioactifs de père en fils … Un certain nombre de noyaux radioactifs naturels sont présent[...]
Décroissances multiples …
Cas de la décroissance des déchets radioactifs du nucléaire En dehors des filiations radioactives[...]
Equilibre radioactif
Des équilibres aussi vieux que la Terre. On appelle filiation radioactive la série de désintégrat[...]
QCM Filiation Uranium
QCM sur la famille radioactive de l’uranium L’uranium naturel contient de nos jours 9[...]